How accurate do long-range (≥10yr) forecasts tend to be, and how much should we rely on them?
As an initial exploration of this question, I sought to study the track record of long-range forecasting exercises from the past. Unfortunately, my key finding so far is that it is difficult to learn much of value from those exercises, for the following reasons:
- Long-range forecasts are often stated too imprecisely to be judged for accuracy. [More]
- Even if a forecast is stated precisely, it might be difficult to find the information needed to check the forecast for accuracy. [More]
- Degrees of confidence for long-range forecasts are rarely quantified. [More]
- In most cases, no comparison to a “baseline method” or “null model” is possible, which makes it difficult to assess how easy or difficult the original forecasts were. [More]
- Incentives for forecaster accuracy are usually unclear or weak. [More]
- Very few studies have been designed so as to allow confident inference about which factors contributed to forecasting accuracy. [More]
- It’s difficult to know how comparable past forecasting exercises are to the forecasting we do for grantmaking purposes, e.g. because the forecasts we make are of a different type, and because the forecasting training and methods we use are different. [More]
We plan to continue to make long-range quantified forecasts about our work so that, in the long run, we might learn something about the feasibility of long-range forecasting, at least for our own case. [More]
1. Challenges to learning from historical long-range forecasting exercises
Most arguments I’ve seen about the feasibility of long-range forecasting are purely anecdotal. If arguing that long-range forecasting is feasible, the author lists a few example historical forecasts that look prescient in hindsight. But if arguing that long-range forecasting is difficult or impossible, the author lists a few examples of historical forecasts that failed badly. How can we do better?
The ideal way to study the feasibility of long-range forecasting would be to conduct a series of well-designed prospective experiments testing a variety of forecasting methods on a large number of long-range forecasts of various kinds. However, doing so would require us to wait ≥10 years to get the results of each study and learn from them.
To learn something about the feasibility of long-range forecasting more quickly, I decided to try to assess the track record of long-range forecasts from the past. First, I searched for systematic retrospective accuracy evaluations for large collections of long-range forecasts. I identified a few such studies, but found that they all suffered from many of the limitations discussed below.[1]E.g. Kott & Perconti (2018); Fye et al. (2013); Albright (2002), which I previously discussed here; Parente & Anderson-Parente (2011).
I also collected past examples of long-range forecasting exercises I might evaluate for accuracy myself, but quickly determined that doing so would require more effort than the results would likely be worth. Finally, I reached out to the researchers responsible for a large-scale retrospective analysis with particularly transparent methodology,[2]This was Fye et al. (2013). See Mullins (2012) for an extended description of the data collection and analysis process, and attached spreadsheets of all included sources and forecasts and how they were evaluated in the study. and commissioned them to produce a follow-up study focused on long-range forecasts. Its results were also difficult to learn from, again for some of the reasons discussed below (among others).[3]The commissioned follow-up study is Mullins (2018). A few notes on this study: The study was pre-registered at OSF Registries here. Relative to the pre-registration, Mullins (2018) extracted forecasts from a slightly different set of source documents, because one of the planned source documents … Continue reading
1.1 Imprecisely stated forecasts
If a forecast is phrased in a vague or ambiguous way, it can be difficult or impossible to subsequently judge its accuracy.[4]For further discussion of this point, see e.g. Tetlock & Gardner (2015), ch. 3. This can be a problem even for very short-range forecasts, but the challenge is often greater for long-range forecasts, since they often aim to make a prediction about circumstances, technologies, or measures that … Continue reading
For example, consider the following forecasts:[5]The forecasts in this section are taken from the forecasts spreadsheet attached to Mullins (2018). In some cases they are slight paraphrases of the forecasting statements from the source documents.
- From 1975: “By 2000, the tracking and data relay satellite system (TDRSS) will acquire and relay data at gigabit rates.”
- From 1980: “The world’s population will increase 55 percent, from 4.1 billion people in 1975 to 6.35 billion in 2000.”
- From 1977: “The average fuel efficiency of automobiles in the US will be 27 to 29 miles per gallon in 2000.”
- From 1972: “The CO2 concentration will reach 380 ppm by the year 2000.”
- From 1987: “In Germany, in the year 1990, 52.0% of women aged 15 – 64 will be registered as employed.”
- From 1967: “The installed power in the European Economic Community will grow by a factor of a hundred from a programmed 3,700 megawatts in 1970 to 370,000 megawatts in 2000.”
Broadly speaking, these forecasts were stated with sufficient precision to now judge them as correct or incorrect.
In contrast, consider the low precision of these forecasts:
- From 1964: “Operation of a central data storage facility with wide access for general or specialized information retrieval will be in use between 1971 and 1991.” What counts as “a central data storage facility”? What counts as “general or specialized information retrieval”? Perhaps most critically, what counts as “wide access”? Given the steady growth of (what we now call) the internet from the late 1960s onward, this forecast might be considered true for different decades depending on whether we interpret “wide access” to refer to access by thousands, or millions, or billions of people.
- From 1964: “In 2000, general immunization against bacterial and viral diseases will be available.” What is meant by “general immunization?” Did the authors mean a universal vaccine? Did they mean widely-delivered vaccines protecting against several important and common pathogens? Did they mean a single vaccine that protects against several pathogens?
- From 1964: “In 2000, automation will have advanced further, from many menial robot services to sophisticated, high-IQ machines.” What counts as a “menial robot service,” and how many count as “many”? How widely do those services need to be used? What is a high-IQ machine? Would a machine that can perform well on IQ tests but nothing else count? Would a machine that can outperform humans on some classic “high-IQ” tasks (e.g. chess-playing) count?
- From 1964: “Reliable weather forecasts will be in use between 1972 and 1988.” What accuracy score counts as “reliable”?
- From 1983: “Between 1983 and 2000, large corporate farms that are developed and managed by absentee owners will not account for a significant number of farms.” What counts as a “large” corporate farm? What counts as a “significant number”?
In some cases, even an imprecisely phrased forecast can be judged as uncontroversially true or false, if all reasonable interpretations are true (or false). But in many cases, it’s impossible to determine whether a forecast should be judged as true or false.
Unfortunately, it can often require substantial skill and effort to transform an imprecise expectation into a precisely stated forecast, especially for long-range forecasts.[6]Technically, it should be possible to transform almost any imprecise forecast into a precise forecast using a “human judge” approach, but this can often be prohibitively expensive. In a “human judge” approach, one would write down an imprecise forecast, perhaps along with … Continue reading
In such cases, one can choose to invest substantial effort into improving the precision of one’s forecasting statement, perhaps with help from someone who has developed substantial expertise in methods for addressing this difficulty (e.g. the “Questions team” at Good Judgment Inc.). Or, one can make the forecast despite its imprecision, to indicate something about one’s expectations, while understanding that it may be impossible to later judge as true or false.
Regardless, the frequent imprecision of historical long-range forecasts makes it difficult to assess them for accuracy.
1.2 Practically uncheckable forecasts
Even if a forecast is stated precisely, it might be difficult to check for accuracy if the information needed to judge the forecast is non-public, difficult to find, untrustworthy, or not available at all. This can be an especially common problem for long-range forecasts, for example because variables that are reliably measured (e.g. by a government agency) when the forecast is made might no longer be reliably measured at the time of the forecast’s “due date.”
For example, in the study we recently commissioned,[7]See the forecasts spreadsheet attached to Mullins (2018). the following forecasts were stated with relatively high precision, but it was nevertheless difficult to find reliable sources of “ground truth” information that could be used to judge the exact claim of the original forecast:
- From 1967: “By the year 2000, the US will include approximately 232 million people age 14 and older.” The commissioned study found two “ground truth” sources for judging this forecast, but some guesswork was still required because the two sources disagreed with each other substantially, and one source had info on the population of those 15 and older but not of those 14 and older.
- From 1980: “In 2000, 400 cities will have passed the million population mark.” In this case there is some ambiguity about what counts as a city, but even if we set that aside, the commissioned study found two “ground truth” sources for judging this forecast, but some guesswork was still required because those sources included figures for some years (implying particular average trends that could be extrapolated) but not for 2000 exactly.
1.3 Non-quantified degrees of confidence
In most forecasting exercises I’ve seen, forecasters provide little or no indication of how confident they are in each of their forecasts, which makes it difficult to assess their overall accuracy in a meaningful way. For example, if 50% of a forecaster’s predictions are correct, we would assess their accuracy very differently if they made those forecasts with 90% confidence vs. 50% confidence. If degrees of confidence are not quantified, there is no way to compare the forecaster’s subjective likelihoods to the objective frequencies of events.[8]One recent proposal is to infer forecasters’ probabilities from their imprecise forecasting language, as in Lehner et al. (2012). I would like to see this method validated more extensively before I rely on it.
Unfortunately, in the long-range forecasting exercises I’ve seen, degrees of confidence are often not mentioned at all. If they are mentioned, forecasters typically use imprecise language such as “possibly” or “likely,” terms which can be used to refer to hugely varying degrees of confidence.[9]E.g. see figure 18 in chapter 12 of Heuer (1999); a replication of that study by Reddit.com user zonination here; Wheaton (2008); Mosteller & Youtz (1990); Mauboussin & Mauboussin (2018) (original results here); table 1 of Mandel (2015). I haven’t vetted these studies. Such imprecision can sometimes lead to poor decisions,[10]Tetlock & Gardner (2015), ch. 3, gives the following (possible) example: In 1961, when the CIA was planning to topple the Castro government by landing a small army of Cuban expatriates at the Bay of Pigs, President John F. Kennedy turned to the military for an unbiased assessment. The Joint … Continue reading and means that such forecasts cannot be assessed using calibration and resolution measures of accuracy.
1.4 No comparison to a baseline method or null model is feasible
One way to make a large number of correct forecasts is to make only easy forecasts, e.g. “in 10 years, world population will be larger than 5 billion.” One can also use this strategy to appear impressively well-calibrated, e.g. by making forecasts like “With 50% confidence, when I flip this fair coin it will come up heads.” And because forecasts can vary greatly in difficulty, it can be misleading to compare the accuracy of forecasters who made forecasts about different phenomena.[11]One recent proposal for dealing with this problem is to use Item Response Theory, as described in Bo et al. (2017): The conventional estimates of a forecaster’s expertise (e.g., his or her mean Brier score, based on all events forecast) are content dependent, so people may be assigned higher or … Continue reading
For example, forecasters making predictions about data-rich domains (e.g. sports or weather) might have better Brier scores than forecasters making predictions about data-poor domains (e.g. novel social movements or rare disasters), but that doesn’t mean that the sports and weather forecasters are better or “more impressive” forecasters — it may just be that they have limited themselves to easier-to-forecast phenomena.
To assess the ex ante difficulty of some set of forecasts, one could compare the accuracy of a forecasting exercises’ effortfully produced forecasts against the accuracy of forecasts about the same statements produced by some naive “baseline” method, e.g. a simple poll of broadly educated people (conducted at the time of the original forecasting exercise), or a simple linear extrapolation of the previous trend (if time series data are available for the phenomenon in question). Unfortunately, such naive baseline comparisons are often unavailable.
Even if no comparison to the accuracy of a naive baseline method is available, one can sometimes compare the accuracy of a set of forecasts to the accuracy predicted by a “null model” of “random” forecasts. For example, for the forecasting tournaments described in Tetlock (2005), all forecasting questions came with answer options that were mutually exclusive and mutually exhaustive, e.g. “Will [some person] still be President on [some date]?” or “Will [some state’s] borders remain the same, expand, or contract by [some date]?”[12]See the Methodological Appendix of Tetlock (2005).
Because of this, Tetlock knew the odds that a “dart-throwing chimp” (i.e. a random forecast) would get each question right (50% chance for the first question, 1/3 chance for the second question). Then, he could compare the accuracy of expert forecasters to the accuracy of a random-forecast “null model.” Unfortunately, the forecasting questions of the long-range forecasting exercises I’ve seen are rarely set up to allow for the construction of a null model to compare against the (effortful) forecasts produced by the forecasting exercise.[13]This includes the null models used in Fye et al. (2013) and Mullins (2018), which I don’t find convincing.
1.5 Unclear or weak incentives for accuracy
For most long-range forecasting exercises I’ve seen, it’s either unclear how much incentive there was for forecasters to strive for accuracy, or the incentives for accuracy seem clearly weak.
For example, in many long-range forecasting exercises, there seems to have been no concrete plan to check the accuracy of the study’s forecasts at a particular time in the future — and in fact, the forecasts from even the most high-profile long-range forecasting studies I’ve seen were never checked for accuracy (as far as I can tell), at least not by anyone associated with the original study or funded by the same funder or funder(s). Without a concrete plan to check the accuracy of the forecasts, how strong could the incentive for forecaster accuracy be?
Furthermore, long-range forecasting exercises are rarely structured as forecasting tournaments, with multiple individuals, groups, or methods competing to make the most accurate forecasts about the same forecasting questions (or heavily overlapping sets of forecasting questions). As such, there’s no way to compare the accuracy of one individual or group or method against another, and again it’s unclear whether the forecasters had much incentive to strive for accuracy.
Also, some studies that were set up to eventually check the accuracy of the forecasts made didn’t use a scoring rule that reliably incentivized reporting one’s true probabilities, i.e. a proper scoring rule.
1.6 Weak strategy for causal identification
Even if a study passes the many hurdles outlined above, and there are clearly demonstrated accuracy differences between different forecasting methods, it can still be difficult to learn about which factors contributed to those accuracy differences if the study was not structured as a randomized controlled trial, and no other strong causal identification strategy was available.[14]On the tricky challenge of robust causal identification from observational data, see e.g. Athey & Imbens (2017) and Hernán & Robins (forthcoming).
1.7 Unclear relevance to our own long-range forecasting
I haven’t yet found a study that (1) evaluates the accuracy of a large collection of somewhat-varied[15]By “somewhat varied,” I mean to exclude studies that are e.g. limited to forecasting variables for which substantial time series data is available, or variables in a very narrow domain such as a handful of macroeconomic indicators or a handful of environmental indicators. long-range (≥10yr) forecasts and that (2) avoids the limitations above. If you know of such a study, please let me know.
Tetlock’s “Expert Political Judgment” project (EPJ; Tetlock 2005) and his “Good Judgment Project” (GJP; Tetlock & Gardner 2015) might come closest to satisfying those criteria, and that is a major reason we have prioritized learning what we can from Tetlock’s forecasting work specifically (e.g. see here) and have supported his ongoing research.
Tetlock’s work hasn’t focused on long-range forecasting specifically, but because Tetlock’s work largely (but not entirely) avoids the other limitations above, I will briefly explore what I think we can and can’t learn from his work about the feasibility of long-range forecasting, and use it to explore the more general question of how studies of long-range forecasting can be of unclear relevance to our own forecasting even when they largely avoid the other limitations discussed above.
1.7.1 Tetlock, long-range forecasting, and questions of relevance
Most GJP forecasts had time horizons of 1-6 months,[16]See figure 3 of this December 2015 draft of a paper eventually published (without that figure) as Friedman et al. (2018). and thus can tell us little about the feasibility of long-range (≥10yr) forecasting.[17]Despite this, I think we can learn a little from GJP about the feasibility of long-range forecasting. Good Judgment Project’s Year 4 annual report to IARPA (unpublished), titled “Exploring the Optimal Forecasting Frontier,” examines forecasting accuracy as a function of … Continue reading
In Tetlock’s EPJ studies, however, forecasters were asked a variety of questions with forecasting horizons of 1-25 years. (Forecasting horizons of 1, 3, 5, 10, or 25 years were most common.) Unfortunately, by the time of Tetlock (2005), only a few 10-year forecasts (and no 25-year forecasts) had come due, so Tetlock (2005) only reports accuracy results for forecasts with forecasting horizons he describes as “short-term” (1-2 years) and “long-term” (usually 3-5 years, plus a few longer-term forecasts that had come due).[18]Forecasting horizons are described under “Types of Forecasting Questions” in the Methodological Appendix of Tetlock (2005). The definitions of “short-term” and “long-term” were provided via personal communication with Tetlock, as was the fact that only a few … Continue reading Update from March 2023: Further evidence about the long-range forecasts from EPJ has now been published in Tetlock et al. (2023).
The differing accuracy scores for short-term vs. long-term forecasts in EPJ are sometimes used to support a claim that the accuracy of expert predictions declines toward chance five years out.[19]E.g. Tetlock himself says “there is no evidence that geopolitical or economic forecasters can predict anything ten years out beyond the excruciatingly obvious — ‘there will be conflicts’ — and the odd lucky hits that are inevitable whenever lots of forecasters make lots of … Continue reading
While it’s true that accuracy declined “toward” chance five years out, the accuracy differences reported in Tetlock (2005) are not as large as I had assumed upon initially hearing this claim (see footnote for details[20]Tetlock (2005) reports both calibration scores and discrimination (aka resolution) scores, explaining that: “A calibration score of .01 indicates that forecasters’ subjective probabilities diverged from objective frequencies, on average, by about 10 percent; a score of .04, an average gap … Continue reading). Fortunately, we might soon be in a position to learn more about long-range forecasting from the EPJ data, since most EPJ forecasts (including most 25-year forecasts) will have resolved by 2022.[21]Personal communication with Phil Tetlock. And according to the Acknowledgements section at the back of Tetlock (2005), all EPJ forecasts will come due by 2026.
Perhaps more importantly, how analogous are the forecasting questions from EPJ to the forecasting questions we face as a grantmaker, and how similar was the situation of the EPJ forecasters to the situation we find ourselves in?
For context, some (paraphrased) representative example “long-term” forecasting questions from EPJ include:[22]Here is an abbreviated summary of EPJ’s forecasting questions, drawing and quoting from Tetlock (2005)’s Methodological Appendix: Each expert was asked to make short-term and long-term predictions about “each of four nations (two inside and two outside their domains of expertise) … Continue reading
- Two elections from now, will the current majority in the legislature of [some stable democracy] lose its majority, retain its majority, or strengthen its majority?
- In the next five years, will GDP growth rates in [some nation] accelerate, decelerate, or remain about the same?
- Over the next ten years, will defense spending as a percentage of [some nation’s] expenditures rise, fall, or stay about the same?
- In the next [ten/twenty-five] years, will [some state] deploy a nuclear or biological weapon of mass destruction (according to the CIA Factbook)?
A few observations come to mind as I consider analogies and disanalogies between EPJ’s “long-term” forecasting and the long-range forecasting we do as a grantmaker:[23]Some of these observations overlap with the other limitations listed above.
- For most of our history, we’ve had the luxury of knowing the results from EPJ and GJP and being able to apply them to our forecasting, which of course wasn’t true for the EPJ forecasters. For example, many of our staff know that it’s often best to start one’s forecast from an available base rate, and that many things probably can’t be predicted with better accuracy than chance (e.g. which party will be in the majority two elections from now). Many of our staff have also done multiple hours of explicit calibration training, and my sense is that very few (if any) EPJ forecasters are likely to have done calibration training prior to making their forecasts. Several of our staff have also participated in a Good Judgment Inc. forecasting training workshop.
- EPJ forecasting questions were chosen very carefully, such that they (a) were stated precisely enough to be uncontroversially judged for accuracy, (b) came with prepared answer options that were mutually exclusive and collectively exhaustive (or continuous), (c) were amenable to base rate forecasting (though base rates were not provided to the forecasters), and satisfied other criteria necessary for rigorous study design.[24]On the other criteria, see the Methodological Appendix of Tetlock (2005). In contrast, most of our forecasting questions (1) are stated imprecisely (because the factors that matter most to the grant decision are ~impossible or prohibitively costly to state precisely), (2) are formulated very quickly by the forecaster (i.e. the grant investigator) as they fill out our internal grant write-up template, and thus don’t come with pre-existing answer options, and (3) rarely have clear base rate data to learn from. Overall, this might suggest we should (ignoring other factors) expect lower accuracy than was observed in EPJ, e.g. because we formulate questions and make forecasts about them so quickly. It also means that we are less able to learn from the forecasters we make, because many of them are stated too imprecisely to judge for accuracy.
- I’m unsure whether EPJ questions asked about phenomena that are “intrinsically” easier or harder to predict than the phenomena we try to predict. E.g. party control in established democracies changes regularly and is thus very difficult to predict even one or two elections in advance, whereas some of our grantmaking is premised substantially on the continuation of stable long-run trends. On the other hand, many of our forecasts are (as mentioned above) about phenomena which lack clearly relevant base rate data to extrapolate, or (in some cases) about events that haven’t ever occurred before.
- How motivated were EPJ forecasters to strive for accuracy? Presumably the rigorous setup and concrete plan to measure forecast accuracy provided substantial incentives for accuracy, though on the other hand, the EPJ forecasters knew their answers and accuracy scores would be anonymous. Meanwhile, explicit forecasting is a relatively minor component of Open Phil staffers’ work, and our less rigorous setup means that incentives for accuracy may be weak, but also our (personally identified) forecasts are visible to many other staff.
Similar analogies and disanalogies also arise when comparing our forecasting situation to that of the forecasters who participated in other studies of long-range forecasting. This should not be used an excuse to avoid drawing lessons from studies when we should, but it does mean that it may be tricky to assess what we should learn about our own situation from even very well-designed studies of long-range forecasting.
2. Our current attitude toward long-range forecasting
Despite our inability to learn much (thus far) about the feasibility of long-range forecasting, and therefore also about best practices for long-range forecasting, we plan to continue to make long-range quantified forecasts about our work so that, in the long run, we might learn something about the feasibility of long-range forecasting, at least for our own case. We plan to say more in the future about what we’ve learned about forecasting in our own grantmaking context, especially after a larger number of our internal forecasts have come due and then been judged for accuracy.
Footnotes
| 1 | E.g. Kott & Perconti (2018); Fye et al. (2013); Albright (2002), which I previously discussed here; Parente & Anderson-Parente (2011). | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | This was Fye et al. (2013). See Mullins (2012) for an extended description of the data collection and analysis process, and attached spreadsheets of all included sources and forecasts and how they were evaluated in the study. | |||||||||||||||
| 3 | The commissioned follow-up study is Mullins (2018). A few notes on this study:
Since Mullins (2018) is modeled after Fye et al. (2013), we knew in advance it would have several of the limitations described in this post, but we hoped to learn some things from it anyway, especially given the planned availability of the underlying raw data. Unfortunately, upon completion we discovered additional limitations of the study. For example, Mullins (2018) implicitly interprets all forecasts as “timing forecasts” of the form “event X will first occur in approximately year Y.” This has some advantages (e.g. allowing one to operationalize some notion of “approximately correct”), but it also leads to counterintuitive judgments in many cases:
There are other limits to the data and analysis in Mullins (2018), and we don’t think one should draw major substantive conclusions from it. It may, however, be a useful collection of long-range forecasts that could be judged and analyzed for accuracy using alternate methods. My thanks to Kathleen Finlinson and Bastian Stern for their help evaluating this report. | |||||||||||||||
| 4 | For further discussion of this point, see e.g. Tetlock & Gardner (2015), ch. 3. This can be a problem even for very short-range forecasts, but the challenge is often greater for long-range forecasts, since they often aim to make a prediction about circumstances, technologies, or measures that aren’t yet well-defined at the time the forecast is made. | |||||||||||||||
| 5 | The forecasts in this section are taken from the forecasts spreadsheet attached to Mullins (2018). In some cases they are slight paraphrases of the forecasting statements from the source documents. | |||||||||||||||
| 6 | Technically, it should be possible to transform almost any imprecise forecast into a precise forecast using a “human judge” approach, but this can often be prohibitively expensive. In a “human judge” approach, one would write down an imprecise forecast, perhaps along with some accompanying material about motivations and reasoning and examples of what would and wouldn’t satisfy the intention of the forecast, and then specify a human judge (or panel of judges) who will later decide whether one’s imprecise forecast should be judged true or false (or, each judge could give a Likert-scale rating of “how accurate” or “how clearly accurate” the forecast was). Then, one can make a precise forecast about the future judgment of the judge(s). The precise forecast, then, would be a forecast both about the phenomenon one wishes to forecast, and about the psychology and behavior of the judge(s). Of course, one’s precise forecast must also account for the possibility that one or more judges will be unwilling or unable to provide a judgment at the required time.
An example of this “human judge” approach is the following forecast posted to the Metaculus forecasting platform: “Will radical new ‘low-energy nuclear reaction’ technologies prove effective before 2019?” In this case, the exact (but still somewhat imprecise) forecasting statement was: “By Dec. 31, 2018, will Andrea Rossi/Leonardo/Industrial Heat or Robert Godes/Brillouin Energy have produced fairly convincing evidence (> 50% credence) that their new technology […] generates substantial excess heat relative to electrical and chemical inputs?” Since there remains some ambiguity about e.g. what should count as “convincing evidence,” the question page also specifies that “The bet will be settled by [Huw] Price and [Carl] Shulman by New Years Eve 2018, and in the case of disagreement shall defer to majority vote of a panel of three physicists: Anthony Aguirre, Martin Rees, and Max Tegmark.” | |||||||||||||||
| 7 | See the forecasts spreadsheet attached to Mullins (2018). | |||||||||||||||
| 8 | One recent proposal is to infer forecasters’ probabilities from their imprecise forecasting language, as in Lehner et al. (2012). I would like to see this method validated more extensively before I rely on it. | |||||||||||||||
| 9 | E.g. see figure 18 in chapter 12 of Heuer (1999); a replication of that study by Reddit.com user zonination here; Wheaton (2008); Mosteller & Youtz (1990); Mauboussin & Mauboussin (2018) (original results here); table 1 of Mandel (2015). I haven’t vetted these studies. | |||||||||||||||
| 10 | Tetlock & Gardner (2015), ch. 3, gives the following (possible) example:
| |||||||||||||||
| 11 | One recent proposal for dealing with this problem is to use Item Response Theory, as described in Bo et al. (2017):
I have not evaluated this approach in detail and would like to see it critiqued and validated by other experts. On this general challenge, see also the discussion of “Difficulty-adjusted probability scores” in the Technical Appendix of Tetlock (2005). | |||||||||||||||
| 12 | See the Methodological Appendix of Tetlock (2005). | |||||||||||||||
| 13 | This includes the null models used in Fye et al. (2013) and Mullins (2018), which I don’t find convincing. | |||||||||||||||
| 14 | On the tricky challenge of robust causal identification from observational data, see e.g. Athey & Imbens (2017) and Hernán & Robins (forthcoming). | |||||||||||||||
| 15 | By “somewhat varied,” I mean to exclude studies that are e.g. limited to forecasting variables for which substantial time series data is available, or variables in a very narrow domain such as a handful of macroeconomic indicators or a handful of environmental indicators. | |||||||||||||||
| 16 | See figure 3 of this December 2015 draft of a paper eventually published (without that figure) as Friedman et al. (2018). | |||||||||||||||
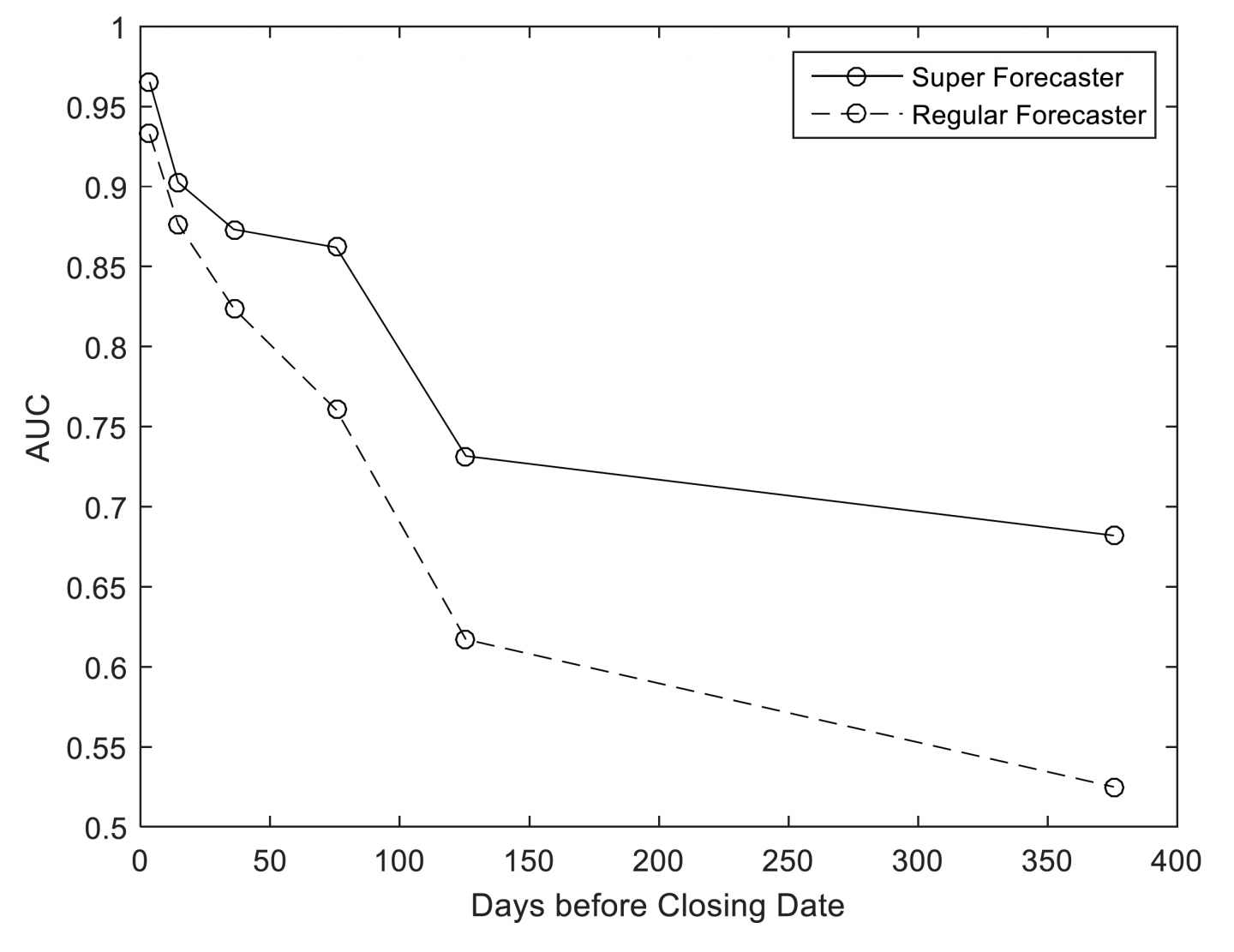
| 17 | Despite this, I think we can learn a little from GJP about the feasibility of long-range forecasting. Good Judgment Project’s Year 4 annual report to IARPA (unpublished), titled “Exploring the Optimal Forecasting Frontier,” examines forecasting accuracy as a function of forecasting horizon in this figure (reproduced with permission):
This chart uses an accuracy statistic known as AUC/ROC (see Steyvers et al. 2014) to represent the accuracy of binary, non-conditional forecasts, at different time horizons, throughout years 2-4 of GJP. Roughly speaking, this chart addresses the question: “At different forecasting horizons, how often (on average) were forecasters on ‘the right side of maybe’ (i.e. above 50% confidence in the binary option that turned out to be correct), where 0.5 represents ‘no better than chance’ and 1 represents ‘always on the right side of maybe’?” For our purposes here, the key results shown above are, roughly speaking, that (1) regular forecasters did approximately no better than chance on this metric at ~375 days before each question closed, (2) superforecasters did substantially better than chance on this metric at ~375 days before each question closed, (3) both regular forecasters and superforecasters were almost always “on the right side of maybe” immediately before each question closed, and (4) superforecasters were roughly as accurate on this metric at ~125 days before each question closed as they were at ~375 days before each question closed. If GJP had involved questions with substantially longer time horizons, how quickly would superforecaster accuracy declined with longer time horizons? We can’t know, but an extrapolation of the results above is at least compatible with an answer of “fairly slowly.” Of course there remain other questions about how analogous the GJP questions are to the types of questions that we and other actors attempt to make long-range forecasts about. | |||||||||||||||
| 18 | Forecasting horizons are described under “Types of Forecasting Questions” in the Methodological Appendix of Tetlock (2005). The definitions of “short-term” and “long-term” were provided via personal communication with Tetlock, as was the fact that only a few 10-year forecasts could be included in the analysis of Tetlock (2005). | |||||||||||||||
| 19 | E.g. Tetlock himself says “there is no evidence that geopolitical or economic forecasters can predict anything ten years out beyond the excruciatingly obvious — ‘there will be conflicts’ — and the odd lucky hits that are inevitable whenever lots of forecasters make lots of forecasts. These limits on predictability are the predictable results of the butterfly dynamics of nonlinear systems. In my EPJ research, the accuracy of expert predictions declined toward chance five years out” (Tetlock & Gardner 2015, p. 243). | |||||||||||||||
| 20 | Tetlock (2005) reports both calibration scores and discrimination (aka resolution) scores, explaining that: “A calibration score of .01 indicates that forecasters’ subjective probabilities diverged from objective frequencies, on average, by about 10 percent; a score of .04, an average gap of 20 percent. A discrimination score of .01 indicates that forecasters, on average, predicted about 6 percent of the total variation in outcomes; a score of .04, that they captured 24 percent” (Tetlock 2005, ch. 2). See the book’s Technical Appendix for details on how Tetlock’s calibration and discrimination scores are computed.
Given this scoring system, Tetlock’s results on the accuracy of short-term vs. long-term forecasts are:
The data above are from figure 2.4 of Tetlock (2005). I’ve renamed “dilettantes” to “non-experts.” See also this spreadsheet, which contains additional short-term vs. long-term accuracy comparisons in data points estimated from figure 3.2 of Tetlock (2005) using WebPlotDigitizer. See ch. 3 and the Technical Appendix of Tetlock (2005) for details on how to interpret these data points. Also note that there is a typo in the caption for figure 3.2; I confirmed with Tetlock that the phrase which reads “long-term (1, 2, 5, 7…)” should instead be “long-term (1, 3, 5, 7…).” | |||||||||||||||
| 21 | Personal communication with Phil Tetlock. And according to the Acknowledgements section at the back of Tetlock (2005), all EPJ forecasts will come due by 2026. | |||||||||||||||
| 22 | Here is an abbreviated summary of EPJ’s forecasting questions, drawing and quoting from Tetlock (2005)’s Methodological Appendix:
| |||||||||||||||
| 23 | Some of these observations overlap with the other limitations listed above. | |||||||||||||||
| 24 | On the other criteria, see the Methodological Appendix of Tetlock (2005). |